【数学】岡山県立高校入試突破のために11月にやっておきたいこと
岡山県立高校入試の数学は毎年大問5つから構成されており、試験時間は45分です。
単純に考えると、大問1つあたり9分間の解答時間がありますが、実際には大問ごとに難易度が異なる上、解く本人の得意不得意にも影響されるためそう甘くはありません。
では、効率よく点数をとるためにはどうすれば良いのでしょうか?
〈大問ごとの配点を知っておこう!〉
年度により小問数が違うので多少変動するものの過去5年でみてみると、大問①20~22点、大問②6~10点、大問③10~15点、大問④10~16点、大問⑤13~20点となっており、大問①の配点率が最も高いことが分かります。
〈計算問題や穴埋め問題を優先して確実に解く!〉
数学では大問①から⑤までを通して30問前後出題され、そのほとんどが1問2点であり、3点や4点のものは数問の出題となっています。
つまり、長時間考えて正解した問題と短時間で計算して正解した問題の得点差がほぼないということになります。
ということは、限られた45分という試験時間の中でより高得点を狙うためには、時間がかかる割に高点数をとれない記述問題(証明など)よりも、素早く解くことのできる計算問題や答えに行きつくまでのヒントが途中まで記載されている穴埋め問題を優先して解くと良いでしょう。中3生はこれからの時期どのような勉強をすればよいか
KLCのみなさんはもう少しすると冬期講習に入り、年明け後の1月・2月は過去問演習となります。
11月時点では、試験に出る範囲すべてを習っているわけではないので、最優先は授業内容を確実に頭に入れることです。
そしてそれと同時に、自分の苦手な分野を克服するための自主学習がポイントになります。
ただ模範解答を読みこんで終わりではなく、ノートにまとめるなどして実際に手を動かし、視覚化することで定着率はグッと上がります。
自分が解けなかった問題だけをまとめたノートを作っておくと後々、弱点を復習するときに使うのはそのノートだけで済むので効率的である上、解ける問題を無駄に何度も解くことがなくなるというメリットもあります。【今後の勉強の流れ】
「11月」
冬期講習までに問題集(テキスト)の全分野の演習問題を8割程度は解けるようにしておきましょう。
これまでに間違えた問題だけでもよいので、繰り返し解くことで答えを導き出す手順に慣れておくことが重要です!
ノートに書いて視覚的に残しておくと効果的です。
もしも今実践している勉強法が正しいかどうか分からなければ、担当の先生に質問してみましょう。
実践している勉強法の良いところや改善点を指摘してくれるはずです。
今のうちに自分にとって最適の勉強法を見つけ定着させておきましょう!「冬期講習中」
講習が始まるまでに問題集(テキスト)が8割程度解けるようになっていることが前提であり、冬期講習では不足している知識の穴埋めがメインとなります。
このとき、解けなかった問題は「なぜ解けなかったのか・解けるようになるには何が必要か」をしっかりと考えましょう。
最初は模範解答を読み込み、その後もう1度自力で解いてみて、正解したらその類題を問題集の中から探し解いてみましょう。
必要ならば先生に似たような問題を出題してもらいましょう。
年末までに問題集(テキスト)の基本問題は全て、発展問題は9割以上解けるようにすることが目標です!「年明けから入試まで」
この時期には問題集(テキスト)は9割以上解けることが前提です。
過去問演習の1番の目的は、入試本番を想定して短時間で問題を解けるようにすることです。
演習では本番で余裕を持たせるために、40分程度で解き終えることを目標にしましょう。
もし大問ごとに時間を区切って解く場合は、大問1つにつき8分を制限時間に設定してみてください。入試問題解答のすすめ方と対策
ここからは、過去問を例にして問題の進め方と対策を見ていきましょう。
大問1(H30度入試問題より抜粋)
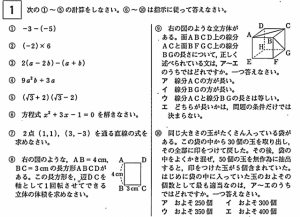
大問1では1年生から3年生で学習する基礎的な計算問題、平面図形や立体図形の面積や体積を求める問題、場合の数・確率、資料の整理などの問題から10問程度出題されます。
どれも難易度はあまり高くありませんが、1問2点×10=20点分の配点(全大問中最多)であるため、ここで点を落とすと致命的となります。
しかし難易度の高い大問2以降にしっかりと時間をかけて点数をとる為にも、ここで8分もかけてしまうと後の余裕がなくなってしまうため、①~⑦は2分、⑧~⑩は③分の計5分程度で解き終えるのが望ましいです。
最も時間がかかると想定される確率の問題では、計算が難しい場合は樹形図を描くとよいでしょう。
また、「資料の整理」の分野からの出題も増えてきているので問題集を解き、各用語の意味や求め方を確実に押さえておく必要があります。
大問2(H29度入試問題より抜粋)

連立方程式の文章問題はほぼ毎年出題されています。
① で連立方程式をつくり、それを解いたものを②で答えるという出題が多いです。
様々な問題に対応できるように日頃から「売買・速さ・水溶液」の問題に取り組み、立式の仕方に慣れておく必要があります。
この大問2も大問1同様の時間で解き終えたいので、問題演習時は制限時間を5分以内に設定して立式から解き終えるまでを速くする練習をしておきましょう。大問3(H30度入試問題より抜粋)
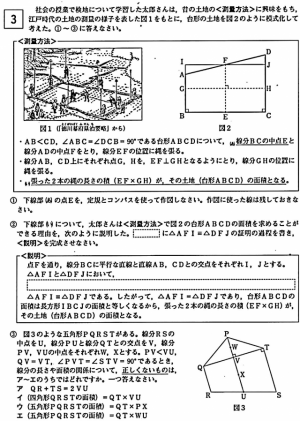
大問3~5のどこかで理科や社会との「融合問題」が出題される傾向があります。
普段見慣れない内容であるがゆえにヒントとなる説明が書かれていたり、空欄補充形式の問題となっていることが多いです。
大問1、大問2で時間的余裕があれば残りの大問は1つあたり10分程度かけてもよい計算になりますが、演習時には8分以内で解くことを目標にしましょう!
①のような作図問題は毎回出題されますが難問であることは少なく、教科書で学ぶ垂直二等分線や角の二等分線、円の接線等の作図が出来ればつまずくことはないでしょう。
②の「証明の空欄補充」では、前後の記載をヒントに考えることが出来るため、ゼロから証明を記述する問題に比べ短時間で済みます。
前半の問題が早く解け、時間に余裕があるのならここで少し長めの考察時間をとってもよいでしょう。
県立高校入試では三角形の合同または相似の証明が頻出であるため問題集の基本問題から発展問題まで幅広く解き多くのパターンに慣れる必要があります。大問4(H25度入試問題より抜粋)
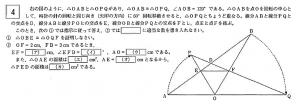
①のように証明を全て記述しないといけない問題が出題されることも少なくありません。
このような問題に当たった時は、後回しにして他の解きやすい問題から解答していくのも戦略です。記述は時間がかかる割に配点が高くないからです。
知っておかないといけないことは、①の証明を後回しにしても②は解答することが出来るということです。
数学は直前の問題の答えを使って次の問題を考えなければならないことが多いですが、証明は記述を後回しにしても結論(この場合だと△OBE≡△OQF)が分かっているので②ではそれを利用すればよいのです。
ここまで問題の進め方についてみてきましたが、大事なことは「時間配分」と「問題選択」をしっかりとすることです。
本番は45分というごく短い時間で、できるだけ多くの問題に正解する必要があるため、解答の手が止まってしまうと他の受験生に差をつけられることになります。
しかし、自分が得意な分野・比較的時間をかけずに解答できる問題を見極める力を本番までに身に着けておけば、反対に他の受験生に差をつけることが出来ます!【最後に】
大問1で出題される計算の基本問題は難なくこなせるように問題集を繰り返し解き、基礎力を固めておきましょう。
また、大問2以降では図形問題が必ず出題されるので、相似・合同の利用や証明、三平方の定理、円の性質、立体図形等を早い段階から復習し、弱点補強に全力を注ぎましょう!
多くの参考書は必要ありません。
メインで使用している問題集の基本問題から発展問題までを何度も解き、間違いを分析して改善を繰り返しましょう。
短期間で劇的な向上は難しい科目ですが、努力はあなたを合格へと近づけてくれます。
一歩ずつ、確実に。











