3学期学年末テストの攻略【中2数学】
いよいよ大事な学年末が近づいてきましたね。
この学年末を受けて通知表がつけられ、入試で使われる内申点が決まります。
学年末テストの数学は平行四辺形の証明がメインテーマになります。証明は記述がややこしいですよね。
特に平行四辺形で一番ややこしいのは定義・定理と条件の違いです。もう既に難しい単語を羅列していますが、
簡単に言うと、
定義・定理とは、「平行四辺形って○○な図形」だよね、といった特徴を表すときに使われるものです。
一方、条件とは「○○になっているとこの四角形は平行四辺形になる」よね、と言いたい場合に使われるものです。
では、この2つがどう違うのか例題を通して確認してみましょう。
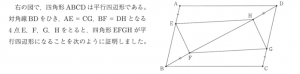
結構複雑な問題になっています。まずはこの問題文をチェックしてみましょう。次の図を見てください。
 平行四辺形という単語が2か所に出てきています。この2つの平行四辺形は意味合いが異なります。前後も含めて見てみると、青いアンダーラインと赤いアンダーラインの部分で少し違うのが分かるでしょうか。
平行四辺形という単語が2か所に出てきています。この2つの平行四辺形は意味合いが異なります。前後も含めて見てみると、青いアンダーラインと赤いアンダーラインの部分で少し違うのが分かるでしょうか。
「○○は平行四辺形である」という文章なら特徴を使い、
「○○は平行四辺形であることを証明」という文章なら条件を言わなければなりません。
さて、この特徴と条件の違いとは何でしょうか。
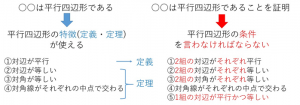 特徴と条件はこのような違いがあります。よく見ると似ていませんか?
特徴と条件はこのような違いがあります。よく見ると似ていませんか?
具体的に言うと、条件は「2組の」や「それぞれ」等、細かく書かれています。なぜこのような違いがあるのでしょうか。次の図で説明していきます。
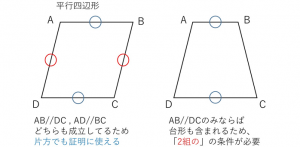 上の図のように、条件がAB//DCだけならADとBCは平行とは言えませんよね。その場合、台形が含まれてしまいます。条件が1つだけなら、その四角形が必ず平行四辺形とは言えないのです。
上の図のように、条件がAB//DCだけならADとBCは平行とは言えませんよね。その場合、台形が含まれてしまいます。条件が1つだけなら、その四角形が必ず平行四辺形とは言えないのです。
状況によって文言の使い分けが必要ですが、最悪条件さえ覚えておけばなんとかなります!少なくともテスト前には条件だけでも覚えておきましょう。
では具体的な使い分けを例題で確認していきましょう。
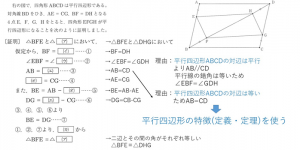
前半は三角形の合同の証明を進めていきます。その際に平行四辺形の特徴を使っています。この証明問題は穴埋め方式ですが、完全記述の証明の場合は上の図で理由と書いている部分等も記述をしっかりしていきましょう。
続きを下の図で見ていきましょう。
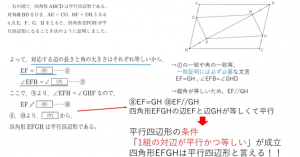 最後のまとめの部分で、平行四辺形の条件を言っています。
最後のまとめの部分で、平行四辺形の条件を言っています。
合同の証明に合同条件が必要なように、平行四辺形と言うには平行四辺形の条件が必要になります。
いかがでしたか?
このようにややこしい文言も、KLCの授業では違いや使う場面を明確に説明していきます。
皆さんも一緒にKLCで学年末テストの成績を上げて次学年に備えましょう!!







