【数学】岡山朝日高校独自入試突破のために１１月にやっておきたいこと

全体概観

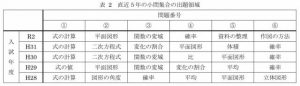
直近５年の出題分野は以下の通りです。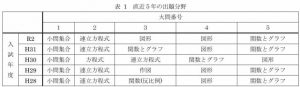

近年の出題傾向を見ると、連立方程式、図形・関数とグラフについては毎年出題されており、攻略することが必須となりますね。では、小問集合も含めてそれぞれの分野ごとにどのような対策を取ればいいのか、実際に入試に出た問題を見ながら確認していきましょう。

【小問集合】

　毎年、大問１では6問の計算問題が出題されています。

例年、第１問は数式の計算を行う問題で統一されていますが、ここ3年でかっこと加減乗除・累乗が入り乱れた、より複雑な計算が取り上げられることが多くなりました。

図 1　H31年度入試大問１①

約分や符号のミスをしないことが求められるのはもちろんですが、図 1のような計算問題は入試の演習で文章題をこなす皆さんならその過程で自然と身についているはずでしょう。むしろこの時期から計算の練習をしているようでは入試に間に合わないです。

第２問以降の二次方程式や関数、図形の問題についても大問２以降の分野を学習する過程でできるようになっていることが理想であるため、この分野についてとりわけ演習をたくさん積む必要はあまりないでしょう。

　しかし、小問集合の中でも確率や資料の整理の分野に関しては毎年出題されていますが、大問の分野では出題されることが稀なため、別に問題演習を積む必要があります。

幸い、大問１には記述解答を求める問題は例年なく、問いの答えだけ記入すればよいので、順列の公式や組み合わせの公式などの高校生で習う公式とその使い方のいくつかを知っておくと、確率の計算に必要な場合の数の計算が楽になるので、もし聞いたことがなければKLCの数学の先生に聞いてみてください。

【連立方程式】

連立方程式も直近５年では必ず出題されています。例えば図２のような問題が出題されています。

図 2 H28年度入試大問２

まずこの問題が方程式の問題であるというところを読み解いて式を2つ作るところを目標に考えます。

式を作るためには、何かの数字を文字で表して立式する必要がありますが、問題文を一見しただけでは、出てくる数字も多く、どの数字を使って立式すればいいかすぐには理解しづらいと思います。

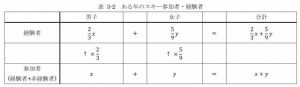
そこで、この問題文に現れる数のもつ性質に着目します。この問題文に現れる数は「男子か女子」「スキー経験者か非経験者」の２つの性質についてどちらかに分類することができます。求めるべき「この年の男子、女子の参加数」をそれぞれ、とおいた後、この2つの性質をそれぞれ横と縦に並べて表を作ってみるとしましょう。

あとは表に当てはめた文字・数字を使って式を作るだけです。

まだ問題文のなかで使っていない、式を作るためのヒントは2つありますよね。「ある年の参加者は男子が女子よりも15人多かった」と「男女のスキー経験者の合計は参加者全体のであった」です。男女の参加者・経験者は既に表しているので簡単に式を作ることができますよね。

このように、方程式を立てる問題では、文章のまま式を作るより、数字の持つ性質に着目・分類すると、わかりやすく式を作ることができます。

　連立方程式で難しい問題となるとこの問題のように、問題文に使われている数字の種類が多くなり、式をはじめから作ろうとしても、うまくいかないのでまずは問題文を読んで式を作る前に必要な数字を文字であらわし、それらの数字の関係を見て、式を作る前の準備として表にまとめるなどしてみるのがよいでしょう。

このタイプの複雑な連立方程式の復習をするのであれば、KLCの4月、6月、8月の志望校判定テストの連立方程式の復習も効果的ですよ。

【図形・関数とグラフ】H31年度入試大問５

最後は、図形・関数とグラフの問いを見てみましょう。関数の分野では中学生で習う関数の中でもっとも複雑ともいえる放物線のグラフが必ずと言っていいほど関連づけて出題されていますが、当然放物線だけ勉強していて解けるような問題が出題されているわけではありません。

この問題では問①や問②は公式通りに解くことができますが、問③や問④になると普段の演習ではなかなか目にしない、台形の面積を3等分する直線の式の導出を求められます。

図形を等分する直線の式を導出する問題で皆さんが多く目にするのは三角形を2等分する直線の式を導出する問題でしょう。その問題なら底辺の中点を通る直線を出せばいいんでしょ？となるところですが、台形でしかも3等分となるとそうはいきませんよね。

このような問題では公式の使い方や図には書かれていない直線、座標の部分まで理解して「面積が3等分」ということを式で表す方法を考えないといけません。

この問のように、関数とグラフの問題も最後には面積や体積を求めるものが多いので図形中心の問題と同様の対策が必要です。

図形と異なる部分で言えば、複数の座標や関数を一つの文字を用いて練習は必要です。ある一点の座標を文字(例えばt)で表したとき、他の座標や関数も同じ文字を使って表せるようにしておきましょう。

関数と図形が関係する類題の演習はKLCの授業で使っているテキストのp232以降あたりを探して取り組んでみましょう。